Hướng Dẫn Chi Tiết Các Cách Tính Diện Tích Hình Vuông Đơn Giản và Chính Xác

Hình vuông là một trong những hình học cơ bản và quen thuộc nhất trong chương trình Toán học mà chúng ta được học từ rất sớm. Việc nắm vững các khái niệm và công thức liên quan đến hình vuông, đặc biệt là cách tính diện tích hình vuông, không chỉ giúp bạn giải quyết các bài toán một cách hiệu quả mà còn đặt nền tảng vững chắc cho việc học Toán ở các cấp độ cao hơn. Bài viết này của Hỗ Trợ FM sẽ cung cấp cho bạn cái nhìn toàn diện về hình vuông, các tính chất đặc trưng và tổng hợp các công thức tính diện tích hình vuông đầy đủ, chính xác nhất, kèm theo các ví dụ minh họa và bài tập thực hành.

I. Lý thuyết cơ bản về hình vuông bạn cần nhớ

Trước khi đi sâu vào tìm hiểu cách tính diện tích hình vuông, việc nắm vững định nghĩa và các tính chất cơ bản của hình vuông là vô cùng quan trọng. Hãy cùng điểm lại những kiến thức nền tảng này.

1. Hình vuông là gì?

Hình vuông là một tứ giác đặc biệt trong hình học phẳng, được định nghĩa bởi các đặc điểm sau:

• Các cạnh bằng nhau: Tất cả bốn cạnh của hình vuông có độ dài bằng nhau.
• Các góc vuông: Bốn góc trong của hình vuông đều là góc vuông, tức là mỗi góc có độ lớn 90 độ.
• Đường chéo: Hai đường chéo của hình vuông bằng nhau, cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau. Đồng thời, mỗi đường chéo là đường phân giác của các góc mà nó đi qua.

Hình vuông là trường hợp đặc biệt của cả hình chữ nhật (vì có 4 góc vuông) và hình thoi (vì có 4 cạnh bằng nhau). Sự đồng nhất về cạnh và góc vuông khiến hình vuông trở thành một hình học cơ bản được ứng dụng rộng rãi trong nhiều lĩnh vực, từ toán học, kiến trúc đến nghệ thuật.

Lý thuyết cần nhớ về hình vuông

2. Các tính chất đặc trưng của hình vuông

Hình vuông sở hữu nhiều tính chất đặc biệt giúp phân biệt nó với các hình học khác và hỗ trợ việc giải toán:

• Cạnh và góc: Tất cả bốn cạnh có cùng độ dài. Tất cả bốn góc đều là góc vuông (90°).
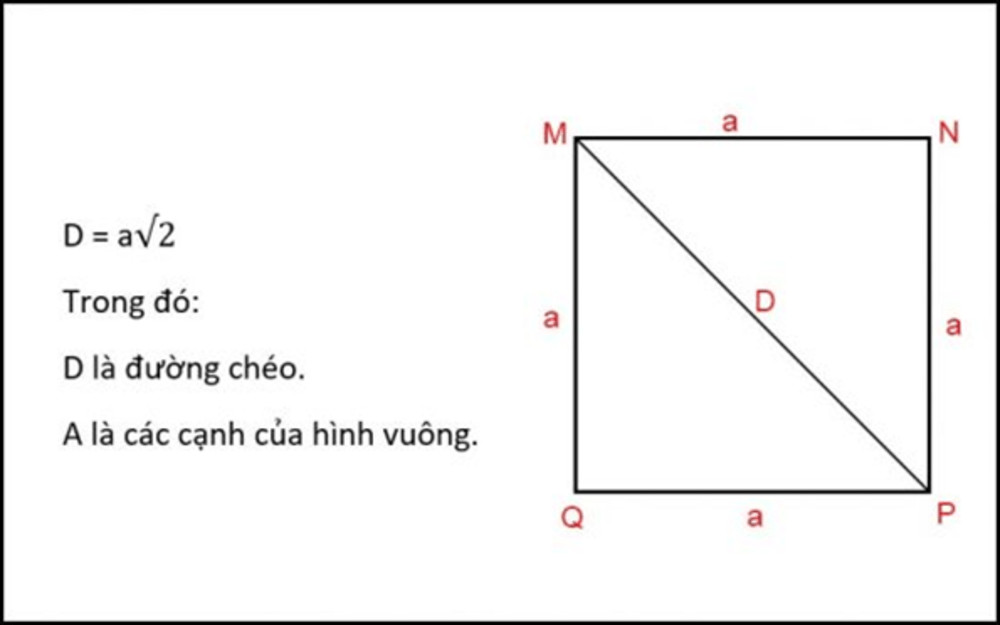
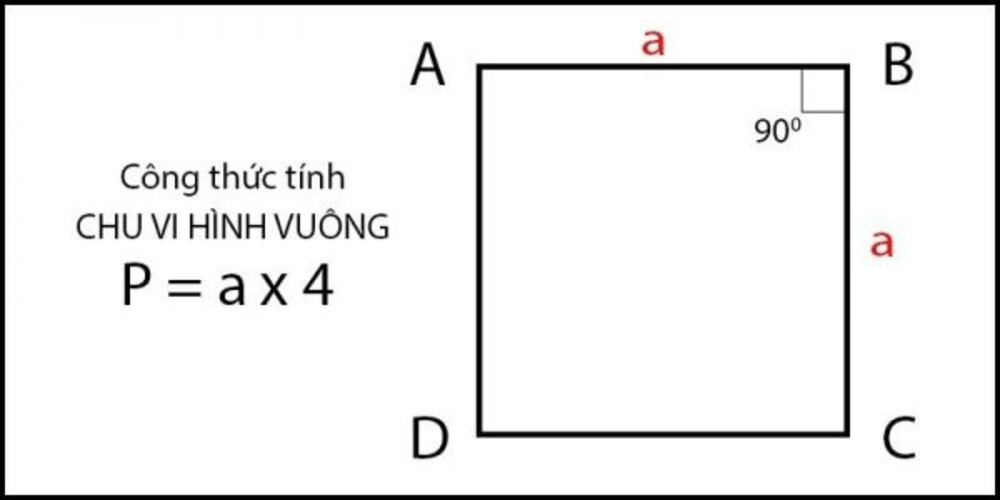
• Đường chéo: Có hai đường chéo bằng nhau. Hai đường chéo cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau. Mỗi đường chéo chia hình vuông thành hai tam giác vuông cân bằng nhau. Độ dài đường chéo (d) được tính bằng công thức: d = a√2 (với a là độ dài cạnh).
• Chu vi và diện tích: Chu vi (P) của hình vuông được tính bằng P = 4 × a. Diện tích (S) của hình vuông được tính bằng S = a × a hoặc S = a².
• Đối xứng: Hình vuông có 4 trục đối xứng (hai đường chéo và hai đường thẳng nối trung điểm các cặp cạnh đối diện). Nó cũng có tâm đối xứng là giao điểm của hai đường chéo.
• Đồng dạng: Tất cả các hình vuông đều đồng dạng với nhau, nghĩa là chúng có cùng tỷ lệ các cạnh và góc.
• Trong không gian: Hình vuông là một hình học phẳng (2 chiều). Nếu bạn kéo dài hình vuông theo chiều vuông góc với mặt phẳng của nó, bạn sẽ tạo ra một hình lập phương (3 chiều).

Việc ghi nhớ các tính chất này sẽ giúp bạn hiểu sâu sắc hơn về hình vuông và áp dụng linh hoạt trong các dạng bài tập khác nhau.

II. Tổng hợp các công thức tính diện tích hình vuông chuẩn xác

Vì hình vuông có các tính chất đặc biệt, nên cách tính diện tích hình vuông cũng có những công thức riêng biệt nhưng rất dễ nhớ. Dưới đây là các công thức đầy đủ và chính xác nhất kèm theo ví dụ minh họa.

1. Cách tính diện tích hình vuông khi biết cạnh (a)

Đây là công thức cơ bản và phổ biến nhất để tính diện tích hình vuông.
Công thức:
Diện tích hình vuông (S) = Cạnh × Cạnh
Hoặc: S = a × a
Hay: S = a²

Công thức tính diện tích hình vuông cạnh a

Ví dụ: Một hình vuông có cạnh là 7 cm. Tính Diện Tích Của Hình Vuông đó.

• Lời giải:
  • Áp dụng công thức: S = a × a
  • S = 7 cm × 7 cm
  • S = 49 cm²
  • Vậy, diện tích của hình vuông là 49 cm².

2. Cách tính diện tích hình vuông khi biết đường chéo (d)

Khi bạn biết độ dài đường chéo của hình vuông, bạn vẫn có thể tính được diện tích mà không cần biết cạnh.
Công thức:
Diện tích hình vuông (S) = (Đường chéo)² / 2
Hoặc: S = d² / 2

Công thức tính diện tích hình vuông khi biết đường chéo

Giải thích: Theo định lý Pythagoras, trong một tam giác vuông cân tạo bởi hai cạnh và một đường chéo, ta có a² + a² = d², suy ra 2a² = d², hay a² = d²/2. Vì S = a², nên S = d²/2.

Ví dụ: Một hình vuông có đường chéo dài 12 cm. Tính diện tích của hình vuông đó.

• Lời giải:
  • Áp dụng công thức: S = d² / 2
  • S = (12 cm)² / 2
  • S = 144 cm² / 2
  • S = 72 cm²
  • Vậy, diện tích của hình vuông là 72 cm².

3. Cách tính diện tích hình vuông khi biết chu vi (P)

Nếu chỉ có thông tin về chu vi, bạn có thể tìm độ dài cạnh trước, sau đó áp dụng công thức tính diện tích.
Công thức:

1. Tính cạnh (a) = Chu vi (P) / 4
2. Tính diện tích (S) = a × a

Công thức tính diện tích hình vuông khi biết chu vi

Ví dụ: Một hình vuông có chu vi là 32 cm. Tính diện tích của hình vuông đó.

• Lời giải:
  • Bước 1: Tính độ dài cạnh (a)
    • a = P / 4 = 32 cm / 4 = 8 cm
  • Bước 2: Tính diện tích (S)
    • S = a × a = 8 cm × 8 cm = 64 cm²
  • Vậy, diện tích của hình vuông là 64 cm².

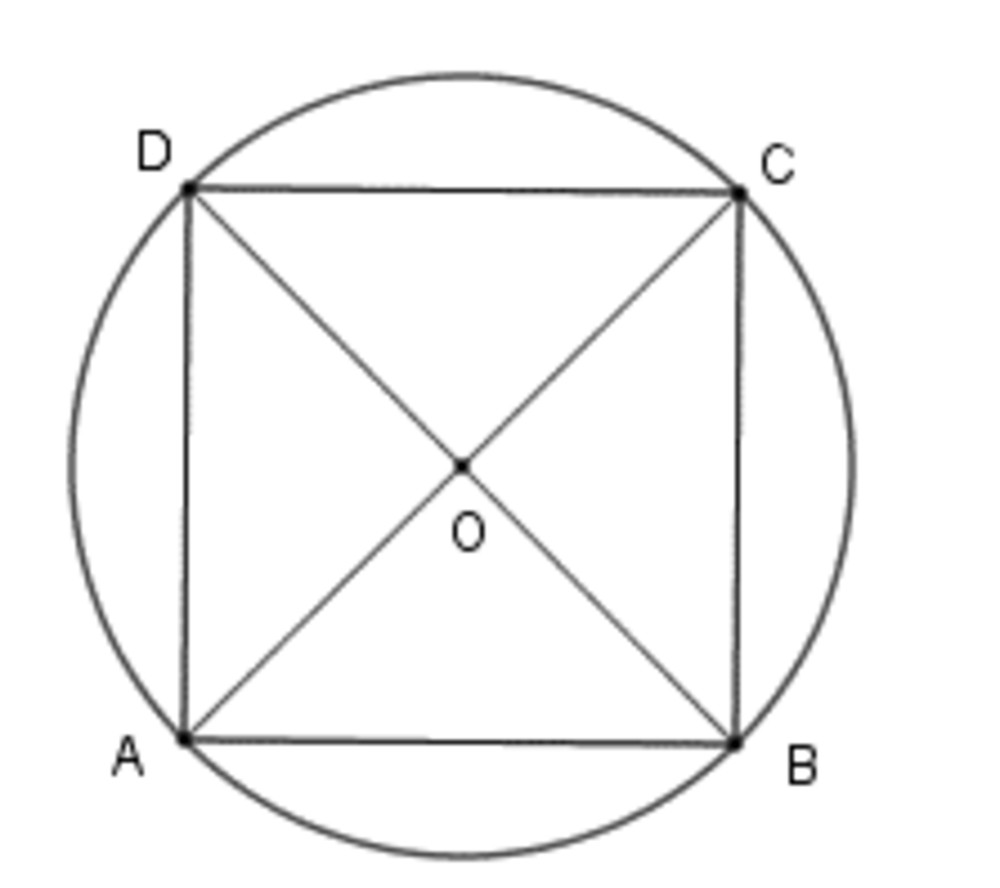
4. Cách tính diện tích hình vuông trong hình tròn ngoại tiếp

Khi một hình vuông được nội tiếp (nằm gọn) trong một hình tròn, đường chéo của hình vuông sẽ chính là đường kính của hình tròn.
Công thức:

1. Tìm đường kính (D) hoặc bán kính (r) của hình tròn. (D = 2r)
2. Đường chéo hình vuông (d) = Đường kính hình tròn (D).
3. Tính diện tích (S) = d² / 2.

Công thức tính diện tích hình vuông trong hình tròn

Ví dụ: Một hình tròn có bán kính là 6 cm. Tính diện tích của hình vuông nội tiếp trong hình tròn đó.

• Lời giải:
  • Bước 1: Tính đường kính của hình tròn.
    • D = 2 × r = 2 × 6 cm = 12 cm
  • Bước 2: Xác định đường chéo của hình vuông.
    • Vì hình vuông nội tiếp hình tròn, đường chéo của hình vuông bằng đường kính của hình tròn, vậy d = 12 cm.
  • Bước 3: Tính diện tích hình vuông.
    • S = d² / 2 = (12 cm)² / 2 = 144 cm² / 2 = 72 cm²
  • Vậy, diện tích của hình vuông là 72 cm².

5. Hướng dẫn tính diện tích hình vuông trong lập trình Pascal

Trong lập trình, đặc biệt là với ngôn ngữ Pascal (thường được học trong môn Tin học lớp 8), việc tính diện tích hình vuông là một bài toán cơ bản.
Dưới đây là một ví dụ đơn giản về cách lập trình để tính diện tích hình vuông trong Pascal: